“Tarea: Informe - Transformaciones lineales”
1. ¿QUÉ ES UNA TRANSFORMACIÓN LINEAL?
En primer lugar, una transformación lineal es una función. Por ser función, tiene su dominio y su condominio, con la particularidad de que éstos son espacios vectoriales.
Tenemos dos espacios vectoriales V y W, y una función que va de V a W. O sea, una regla de asignación que transforma vectores de V en vectores de W. Pero no toda función que transforme vectores de V en vectores de W es una transformación lineal. 
Sean espacios vectoriales sobre un mismo cuerpo K
Una función T de V en W transforma vectores de V en vectores de W
Impondremos condiciones para que T preserva las operaciones de suma de vectores y multiplicación por escalar, esto es, que sea equivalente sumar y multiplicar por escalar las preimágenes en V como las imágenes en W.
Ejemplo
Sean (V, +V , ·V ) y (W, +W , ·W ) dos K- espacios vectoriales. Una función f : V → W se llama una transformaci´on lineal (u homomorfismo, o simplemente morfismo) de V en W si cumple:
i) f(v +V v 0 ) = f(v) +W f(v 0 ) ∀ v, v0 ∈ V. ii)
f(λ ·V v) = λ ·W f(v) ∀ λ ∈ K, ∀ v ∈ V

2. ¿CUÁLES SON LAS CONDICIONES PARA QUE EXISTA UNA TRANSFORMACIÓN LINEAL?
T: V→WT: V→W es una transformación lineal si y sólo si:
1. T(u + v) =T(u)+T(v) ∀u, v ∈VT(u + v)=T(u)+T(v) ∀u, v ∈ V
2. T(k.v) = k.T(v) ∀v∈V, ∀k∈R
Una transformación lineal, a la que llamaremos simplemente T, relaciona a los elementos de dos espacios vectoriales V y W, asignando a cada vector v perteneciente a V un único vector w que pertenece a W, a través de una operación específica.

Condición 1
Se refiere a la adición, para que una transformación T sea lineal, tiene que cumplirse que:
T (v + w) = T (v) + T (w)
-Condición 2
La segunda condición representa la homogeneidad en la multiplicación de un escalar por un vector:
T (cv) = c⋅T (v)
La transformación lineal, tal como su nombre lo indica, se encarga de mapear o transformar elementos de V en elementos de W.
La notación para funciones también se utiliza en el caso de las transformaciones lineales, así, el dominio de V es el conjunto de elementos (vectores) a transformar, mientras que el codominio o recorrido es el conjunto resultante.
Un ejemplo de transformación lineal es:

Para indicar que se va a realizar una transformación se usa la letra T. La transformación se va a aplicar a un vector v cuyas componentes son x e y, el cual se ha representado mediante una matriz de una sola columna. El resultado es otro vector w cuyas componentes son x y 0, también representado mediante una columna matriz.
Por lo tanto, esta es una transformación del espacio vectorial R2 hacia el espacio vectorial R2, que en síntesis se escribe así:
T: R2 → R2
Si tenemos el vector:

La transformación nos devuelve:
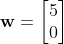
3. AL MENOS CINCO PROPIEDADES O TEOREMAS DE LAS TRANSFORMACIONES LINEALES.
¿Para qué sirven las transformaciones lineales?
En un principio, las transformaciones lineales trabajan con espacios vectoriales, formados por vectores. Muchas veces asociamos los vectores con fuerzas y otras magnitudes físicas, sin embargo en el procesamiento digital de imágenes, un pixel se puede representar por un vector.
En ese caso, la imagen se puede manipular mediante transformaciones lineales convenientes para obtener los efectos deseados, por ejemplo proyectarse, rotarse, hallar la imagen especular o modificar su tamaño sin cambiar las dimensiones relativas.
Las transformaciones lineales también se usan ampliamente en economía y toma de decisiones, por ejemplo para conocer la cantidad de materia prima requerida para fabricar un determinado lote de productos.
El número de piezas necesario para ensamblar los diversos modelos que produce una fábrica, se pueden trabajar mediante un arreglo matricial, como veremos más adelante.
Tipos de transformaciones lineales (clasificación)
Al igual que las funciones, las transformaciones lineales pueden ser:
-Inyectivas o monomorfismos
-Biyectivas o epimorfismos
-Sobreyectivas o isomorfismos
Además están los siguientes tipos:
-Endomorfismos
-Automorfismos.
Transformaciones lineales inyectivas
Sean V y W espacios vectoriales y T una transformación lineal T: V → W. T es inyectiva cuando:
Ker (T) = 0
Transformaciones lineales sobreyectivas
Si V y W son los espacios vectoriales tales que T: V → W, se dice que T es biyectiva cuando:
Im (T) = W
Transformaciones lineales biyectivas
Una transformación lineal T: V → W es biyectiva cuando es a la vez inyectiva y sobreyectiva. Por lo tanto se cumple que:
Ker (T) = 0 e Im (T) = W
Endomorfismos
Son transformaciones lineales en las cuales coinciden el dominio y el codominio.
Automorfismos
Esta clase de transformaciones lineales son endomorfismos biyectivos.
Transformaciones lineales especiales
Operador lineal
Una transformación lineal T: V → V, que va de un espacio vectorial al mismo espacio vectorial se denomina operador lineal.
Transformación cero
Mencionada más arriba, la transformación cero es importante para hallar el kernel de una transformación lineal:
T: V → W tal que T (v) = 0 para cualquier v.
Transformación identidad
T: V → V tal que T (v) = v para cualquier v.
Transformación definida por una matriz
T: V → W tal que T (v) = Av, donde A es una matriz y v es un vector columna.
Función lineal
Las funciones lineales del tipo y = mx son transformaciones lineales. Tomemos por ejemplo y = 3x y veamos si cumple las dos condiciones del comienzo, probando con dos valores a y b cualesquiera:
f (a+b) = 3 (a+b) = 3a + 3b = f(a)+f(b)
f(ka) = 3(ka) = k⋅(3a) =k⋅f(a)
Efectivamente se trata de una transformación lineal.
Ejemplo 1
En muchos problemas de Mecánica necesitamos hallar la proyección de un vector v perteneciente al espacio, sobre un determinado plano. Este vector v puede representar por ejemplo una fuerza.
Supongamos que se desea proyectar el vector v = <x, y, z> sobre el plano xy. Podemos definir una transformación lineal dada por la siguiente matriz:

Cuando la aplicamos al vector v obtenemos un vector cuya componente z se anula. Geométricamente se representa así, con la proyección de v sobre el plano xy como el vector de color rojo con dos componentes.

Teorema 1
Sea T: V→W una transformación lineal. Entonces para todos los vectores u, v, v1,v2,….vn, en V y todos los escalares α1, α2,…. αn:
i. T (0) = 0
ii. T (u-v) =Tu – Tv
iii. T (α1v1 + α2v2 + ….. αnvn) = α1Tv1 + α2Tv2 + …… αnTvn
Teorema 2
Sea V un espacio vectorial de dimensión finita con base B = {v1, v2, ….vn}.
Sean w1, w2, …. wn vectores en W. Suponga que T1 y T2 son dos transformaciones lineales de V en W tales que T1vi = T2vi =wi para i = 1, 2,., n. Entonces para cualquier vector v ϵ V, T1v = T2v; es decir, T1 = T2
Teorema 3
Sea V un espacio vectorial de dimensión finita con base B = {v1, v2, ….vn}.
Sea W un espacio vectorial que contiene los vectores w1, w2, …. wn. Entonces existe una transformación lineal única T: V→W tal queTvi = wi para i 1, 2, …, n.
Teorema 4
Para definir este teorema se deben definir dos conceptos propios de las transformaciones lineales: imagen y núcleo, sea V y W dos espacios vectoriales y sea T: V → W una transformación lineal. Entonces:
i. El núcleo de T, denotado por nu T, está dado por:
nu T = {v ϵ V : Tv = 0}
ii. La imagen de T, denotado por im T, está dado por:
Im T = {w ϵ W: w = Tv para alguna v ϵ V}
Ahora viene la definición del teorema:
Sea T: V→W es una transformación lineal, entonces
i.nu T es un subespacio de V.
ii. Im T es un subespacio de W.
Teorema 5
La imagen del vector –v es igual al opuesto de la imagen de v: T(–v) = –T(v)
Demostración:
T(–v) =T(–1.v) = –1.T(v)=–T(v)
Supongamos una transformación lineal T de V en W, en la cual los vectores v y u pertenecen a V, entonces se cumplen las siguientes propiedades:
Propiedad 1
T (0) = 0
Donde 0 es el vector nulo.
Propiedad 2
T (-v) = – T (v)
Propiedad 3
T (u – v) = T (u) – T(v)
Propiedad 4
Sea v = c1v1 + c2v2 + …. + cnvn
Entonces:
T (c1v1 + c2v2 + …. + cnvn) = c1 T(v1) + c2 T(v2) + …. + cn T(vn)
4. UN EJEMPLO DE UNA TRANSFORMACIÓN LINEAL.
¿Cómo demostrar que T es una transformación lineal?; Donde:
T: P2 --> M2x2
T (ax^2 + bx + c) = (a-b b)
(c+a 2a)
Hay que demostrar que es una aplicación y es lineal.
Que es una aplicación es obvio, a cada polinomio de P2 le corresponde una y solo una matriz de M2x2.
Y para ser lineal debe cumplir dos condiciones:
1) T(p+q) = T(p)+T(q) para todo p,q € P2
2) T(Kp) = k·T(p) para todo p € P2 y todo k€R
Demostración:
Sea p=ax^2+bx+c
q=a'x^2+b'x+c'
T(p+q) = T(ax^2+bx+c + a'x^2 +b'x +c') =
T((a+a')x^2+(b+b')x +(c+c') =
(a+a'-b-b' b+b’ )
(c+c'+a+a' 2a+2a')
·
T(p)+T(q) =T(ax^2+bx+c) + T(a'x^2+b'x+c') =
(a-b b) (a'-b' b') (a+a'-b-b' b+b')
(c+a 2a) + (c'+a' 2a') = (c+c'+a+a' 2a+2a')
5. CÓMO PROBAR ESA TRANSFORMACIÓN LINEAL.
Como vemos los dos resultados son iguales, luego
T(p+q) =T(p)+T(q)
Y la segunda condición será
T(kp) = T(kax^2+kbx+kc) =
(ka-kb kb)
(kc+ka 2ka)·
k·T(p) = (a-b b) (ka-kb kb)
k (c+a 2a) = (kc+ka 2ka)
Los resultados son iguales, luego:
T(kp) = k·T(p)
Y siendo una aplicación y cumpliendo esas dos condiciones se cumple que T es una transformación lineal (o aplicación lineal en otros sitios).
REFERENCIAS
https://aga.frba.utn.edu.ar/definicion-y-propiedades-de-las-transformaciones-lineales/
https://www.uv.mx/personal/aherrera/files/2014/08/21c.-TRANSFORMACIONES-LINEALES-3.pdf
https://dochub.com/a-canola74/ok2BPdERPkOzL6wAxpLrNl/tarea-informe-transformaciones-lineales-pdf?dt=PFPW1sdvZ4sqg5DmoQMy&pg=4
https://www.lifeder.com/transformaciones-lineales/
https://es.wikipedia.org/wiki/Aplicaci%C3%B3n_lineal#Propiedades_de_las_transformaciones_lineales

